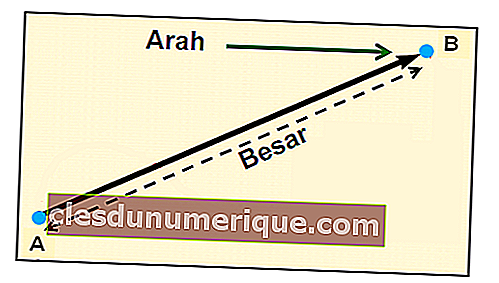
Anteriormente, discutimos o significado dos vetores. Onde pode ser interpretado como um objeto geométrico que tem magnitude e direção, e é marcado com uma seta. Desta vez, exploraremos mais sobre as operações no próprio vetor, que inclui adição e subtração. Bem, como o quê?
Adição e subtração de vetores
Basicamente, existem vários métodos que podem ser usados para realizar operações de adição de vetores, ou seja, o método do triângulo para adicionar dois vetores; o método Tier para a adição de dois vetores; e o método Polygon para a adição de dois ou mais vetores.
Método Triângulo
O método do triângulo é um método de adição de vetor colocando a base do segundo vetor no final do primeiro vetor. A soma dos vetores é um vetor que tem uma base na base do primeiro vetor e uma extremidade no final do segundo vetor.
(Leia também: Compreendendo os vetores em matemática e física)
Suponha que existam dois vetores A e B, então a soma dos dois vetores usando o método do triângulo é a seguinte:

O Método dos Níveis
O método da camada é um método de adicionar dois vetores que são colocados no mesmo ponto de partida, de modo que o resultado dos dois vetores seja a diagonal do nível.
Por exemplo, existem dois vetores A e B, então a soma dos dois vetores usando o método de camada é a seguinte:

Método Poligonal
O método do polígono é um método de adição de dois ou mais vetores. Este método é feito colocando a base do segundo vetor no final do primeiro vetor, em seguida, colocando a base do terceiro vetor no final do segundo vetor e assim por diante.
O resultado da adição desses vetores é um vetor originado na base do primeiro vetor e terminando no final do vetor final.
Suponha que existam três vetores, A, B e C, então a soma dos três vetores usando o método do polígono é a seguinte:

Direito Comutativo e Associativo
A adição de vetores cumpre ambas as leis, ambas comutativas e associativas.
→ Lei Comutativa, o que significa que podemos trocar números e a resposta permanece a mesma para adição ou multiplicação .
→ Lei Associativa, o que significa que podemos agrupar operações numéricas em uma ordem diferente (por exemplo, qual iremos calcular primeiro).
A operação de subtração de vetor é, em princípio, a mesma que a operação de adição de vetor, mas inverte a direção do vetor de redução.
Por exemplo, há uma subtração de dois vetores A e B, então o vetor A menos o vetor B é igual ao vetor A mais o vetor negativo B.
O negativo do vetor B pode ser obtido invertendo o vetor B na direção oposta, de modo que a redução do vetor A pelo vetor B pode ser mostrada pela figura a seguir.
(cenário)
Urgente:
A redução do vetor não segue as leis comutativas
A - B ≠ B - A
A redução do vetor não segue as leis associativas
(A - B) - C ≠ A - (B - C)