Você já viu o movimento de um pêndulo ou mola? Os dois movimentos que você observa são classificados como movimentos harmônicos simples. É um movimento para frente e para trás em torno do ponto de equilíbrio. Se você prestar atenção, o pêndulo tem um ponto de equilíbrio no meio, porque mesmo que sua velocidade diminua, o pêndulo ainda se moverá em torno do ponto de equilíbrio.
O movimento harmônico simples tem amplitude (desvio máximo) e frequência fixas. Este movimento é periódico. Cada movimento ocorrerá repetidamente e regularmente no mesmo intervalo de tempo.
No movimento harmônico simples, a força resultante tem a mesma direção, ou seja, em direção ao ponto de equilíbrio. Essa força é chamada de força restauradora. A quantidade de força de restauração é diretamente proporcional à posição do objeto no ponto de equilíbrio.
Algumas das características desse movimento incluem um gráfico da posição da partícula em função do tempo na forma de um seno ou cosseno. Este movimento também pode ser visto a partir da equação do desvio, equação da velocidade, equação da velocidade e equação da energia do movimento em questão.
(Leia também: Quantidades no conceito de movimento reto)
Com base nessas características, o movimento harmônico simples tem desvio, velocidade, aceleração e energia.
Desvio
O desvio harmônico simples pode ser considerado como a projeção de partículas que se movem em círculos regulares no diâmetro do círculo. Em geral, a equação de desvio neste movimento é a seguinte.
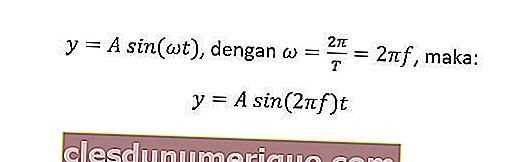
y = desvio de vibrações (m)
ω = velocidade angular (rad / s)
T = período (s)
f = frequência (Hz)
t = tempo (s) de viagem
A = amplitude / desvio máximo (m)
Rapidez
A velocidade é a primeira derivada da posição. No movimento harmônico simples, a velocidade é obtida a partir da primeira derivada da equação de desvio. A equação da velocidade pode ser descrita como segue.

Aceleração
A aceleração de um objeto em movimento harmônico simples pode ser obtida a partir da primeira derivada da equação de velocidade ou da segunda derivada da equação de desvio. A equação de aceleração pode ser obtida como segue.
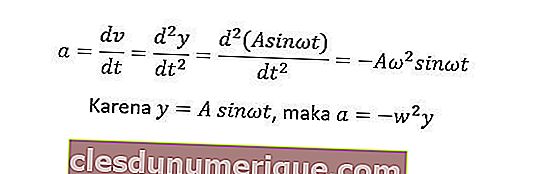
O desvio máximo tem um valor igual à amplitude (y = A), então a aceleração máxima é am = - Aw
Energia
A equação de energia em movimento harmônico simples inclui energia cinética, energia potencial e energia mecânica. A energia cinética do objeto pode ser formulada da seguinte forma.
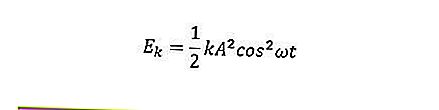
A energia potencial do objeto pode ser formulada da seguinte forma.
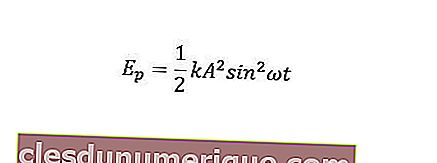
Enquanto isso, a energia mecânica é a soma da energia cinética e da energia potencial.
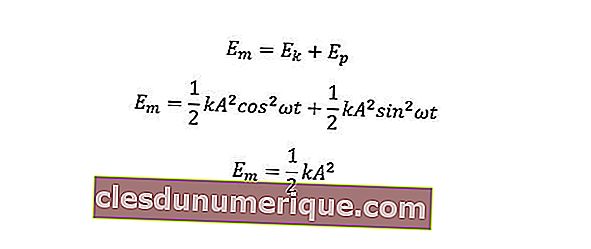
k = valor fixo (N / m)
ω = velocidade angular (rad / s)
A = amplitude (m)
t = tempo (s) de viagem
A quantidade de energia potencial e energia cinética de um objeto movendo harmônicos simples é sempre fixa.









