Só para você saber, as relações também existem na matemática, sabe. Relacionamentos existem no material a respeito de conjuntos. Relacionamentos são regras que conectam membros de um conjunto com outros membros do conjunto. A relação do conjunto A com o conjunto B conecta membros do conjunto A aos membros do conjunto B. Nesta oportunidade, aprenderemos sobre exemplos de relações e suas propriedades, bem como vários exemplos de problemas que podem ajudá-lo a entender melhor este material.
Exemplos de relacionamentos e sua natureza
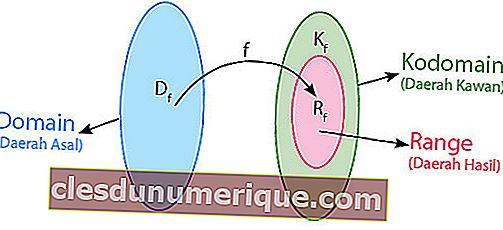
O relacionamento pode ser definido como uma regra que conecta membros da área de origem (domínio) e membros de uma área amiga (codomínio). Em um relacionamento, não há regras especiais que devem ser cumpridas para combinar membros da associação regional com membros de regiões amistosas.
fonte: idschool.net
Cada membro da associação regional de origem pode ter mais de um parceiro ou não ter nenhum. A relação de dois conjuntos pode ser expressa de três maneiras, a saber:
- Diagrama de setas
- Diagrama cartesiano.
- O conjunto de pares consecutivos
A seguir está uma explicação adicional das três maneiras:
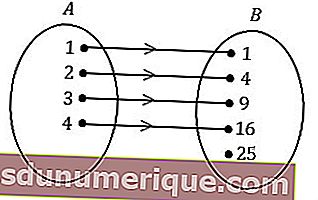
Gráficos de setas
Os gráficos de setas são a maneira mais fácil de expressar um relacionamento. Este diagrama formará um padrão de uma relação na forma de uma seta que mostra a relação dos membros do conjunto A com os membros do conjunto B.
Fonte: maretong.com
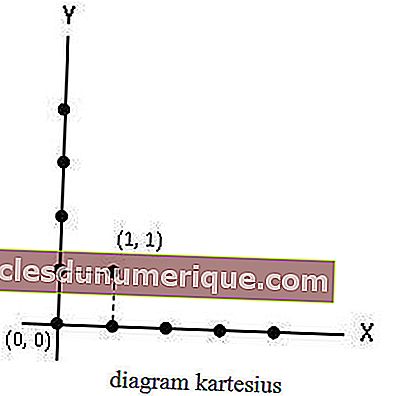
Diagrama cartesiano
O diagrama cartesiano é um diagrama que consiste em um eixo X e um eixo Y. Em um diagrama cartesiano, os membros do conjunto A estão localizados no eixo X, enquanto os membros do conjunto B estão no eixo Y. As relações que conectam o conjunto A a B são indicadas por pontos ou pontos.
Conjunto de pares consecutivos
Uma relação que conecta um conjunto a outro conjunto pode ser representada na forma de um conjunto de pares ordenados. A maneira de escrever é que os membros do conjunto A são escritos primeiro, enquanto os membros do conjunto B, que são os pares, são escritos em segundo lugar.
Exemplos como este:
A = Conjunto mundial, Japão, Coreia, França
Conjunto B = Tóquio, Paris, Jacarta, Seul
Determine o conjunto ordenado de pares por país e capital.
Responda:
{(Mundo, Jacarta), (Japão, Tóquio), (Coréia, Seul), (França, Paris)}
Função
Uma função ou mapeamento é uma relação especial do conjunto A para o conjunto B, com a regra de que cada membro do conjunto A corresponde exatamente um ao membro do conjunto B.
O resultado do mapeamento de domínio para domínio é chamado de intervalo de funções ou área de resultados. Semelhante às relações, as funções também podem ser representadas na forma de diagramas de setas, pares ordenados e diagramas cartesianos.
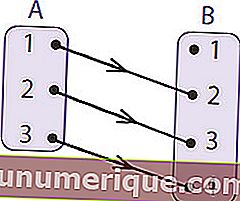
Fonte: rumushitung.com
Para entender melhor, considere a imagem acima. O conjunto A ou área de origem é denominado domínio. O conjunto B, que é uma área amiga, é chamado de codomínio. O membro da área amigável que é o resultado do mapeamento é chamado de área de produção ou intervalo de funções. Portanto, a partir do diagrama de setas acima, pode-se concluir que
- Domínio (D f) é A = {1,2,3}
- Codomínio é B = {1,2,3,4}
- Faixa / Rendimento (R f) é = {2,3,4}
As funções podem ser denotadas com letras minúsculas, como f, g, h, i e assim por diante. A função f mapeia o conjunto A para o conjunto B, então ela pode ser denotada por f (x): A → B.
Um exemplo é a função f que mapeia A para B com a regra f: x → 2x + 2. Pela notação da função, x é um membro do domínio. A função x → 2x + 2 significa que a função f mapeia x para 2x + 2. Portanto, a área de x pela função f é 2x + 2. Portanto, você pode denotá-la como f (x) = 2x +2.
Se a função f: x → ax + b com x é um membro do domínio f, então a fórmula para a função f é
f (x) = ax + b
Exemplo de problemas:
Dada a função f: x → 2x - 2 onde x é um inteiro. Tente determinar o valor de f (3).
Solução:
A função f: x → 2x - 2 pode ser representada por f (x) = 2x - 2
tão,
f (x) = 2x - 2
f (3) = 2 (3) - 2 = 4
Esse é um exemplo de relações e funções em matemática. Você tem alguma dúvida sobre isso? Escreva sua pergunta na coluna de comentários e não se esqueça de compartilhar esse conhecimento.