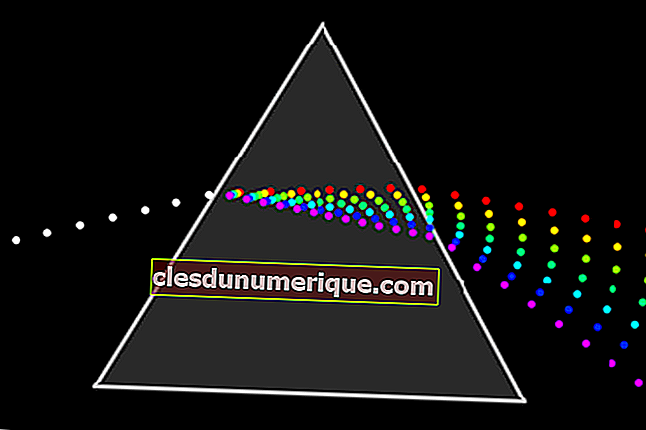
Se você estuda matemática, deve ter ouvido ou estudado trigonometria. Bem, trigonometria é um ramo da matemática que estuda a relação entre o ângulo e os comprimentos laterais de um triângulo, como seno, cosseno e tangente. Tomada literalmente, trigonometria vem do grego, ou seja, trigonon que significa "três ângulos" e metron, que significa "medir". Tal como acontece com vários materiais em matemática, existem fórmulas trigonométricas que você precisa saber.
Nesta ocasião, tentaremos entender vários tipos de fórmulas e também exemplos de seus problemas.
Fórmulas Trigonométricas
O conceito de trigonometria é um conceito importante em triângulos. Os valores trigonométricos são formulados com base na proporção dos lados de um triângulo retângulo. Existem seis valores de razão trigonométrica, a saber, seno (sin), cosseno (cos), tangente (tan), cossecante (cossec), secante (sec) e cotangente (cot). Os seis tipos de valores trigonométricos podem ser determinados comparando os comprimentos laterais com certas regras.
Os usos da trigonometria são muitos, variando de astronomia, geografia, teoria musical, acústica, análise óptica do mercado financeiro, eletrônica, teoria da probabilidade, estatística, biologia, imagens médicas, farmácia, química e muito mais.
Agora, agora é a hora de conhecermos as várias fórmulas trigonométricas desta lição.
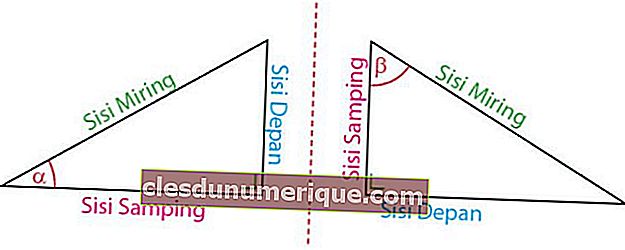
Fonte da imagem: idschool.net
Com base em sua localização em relação ao ângulo, os lados do triângulo - cotovelo são divididos em três tipos, a saber, o lado frontal, o lado lateral e a hipotenusa. O lado frontal é o lado voltado para o canto. O lado está do lado do canto. O lado inclinado está sempre na frente do ângulo de 90o.
Bem, as três funções trigonométricas principais são as funções sin, cos e tan. A definição das três funções com base nos lados e ângulos de um triângulo retângulo pode ser vista na figura e na equação abaixo.
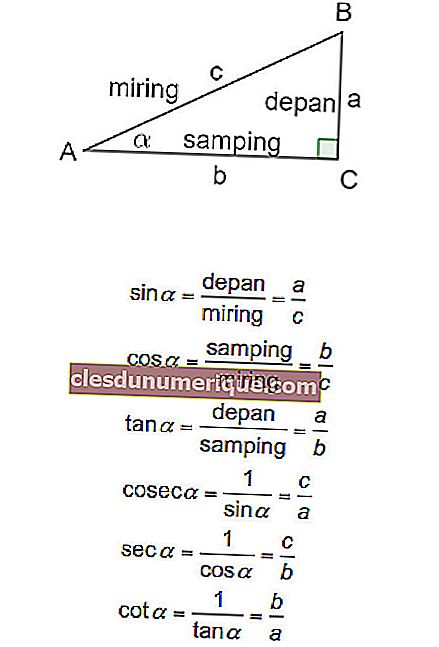
Agora, especificamente para ângulos especiais, os valores trigonométricos são os seguintes:
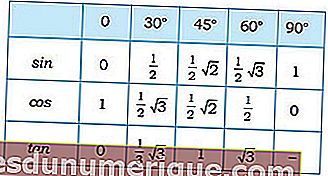
Fonte da imagem: madematics.net
Comparação trigonométrica de ângulos correlacionados
A razão trigonométrica do ângulo relacionado é a extensão do valor trigonométrico básico que é determinado a partir do ângulo do triângulo retângulo. O ângulo de um triângulo retângulo está localizado apenas no quadrante I porque é um ângulo agudo cujo tamanho é de 0 ° - 90 °.
O ângulo central do círculo está entre 0 ° - 360 °. O ângulo é dividido em 4 quadrantes, cada quadrante tem um alcance de 90 °.
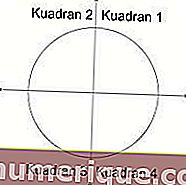
Fonte da imagem: studiobelajar.com
- O quadrante 1 tem um ângulo entre 0 ° - 90 °. Todos os valores de razão trigonométrica são positivos neste quadrante.
- O quadrante 2 tem um ângulo entre 90 ° - 180 °. Neste quadrante, apenas os valores de seno e cossecante são positivos.
- O quadrante 3 tem um ângulo entre 180 ° - 270 °. Neste quadrante, apenas tangentes e cotangentes são positivas.
- O quadrante 4 tem um ângulo entre 270 ° - 360 °. Neste quadrante, apenas o cosseno e a secante são positivos.
Identidade Trigonométrica
O teorema de Pitágoras, ou seja, a2 + b2 = c2 é a base para a preparação de identidades trigonométricas. As identidades trigonométricas expressam a relação de uma função trigonométrica com outras funções trigonométricas.
A soma do seno ao quadrado e do cosseno ao quadrado é igual a um. Se ambos os lados são divididos pelo cosseno ao quadrado, um mais a tangente ao quadrado é igual à secante ao quadrado. Da mesma forma, se ambos os lados são divididos pelo seno ao quadrado, podemos obter um mais a cotangente ao quadrado igual ao cosseno ao quadrado.
Esta é a fórmula de identidade:
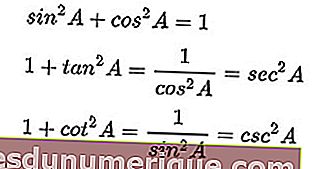
Fonte da imagem: wikipedia.org
Várias outras fórmulas
Existe outra fórmula que você deve saber, a saber:
A fórmula para a soma e diferença dos ângulos:
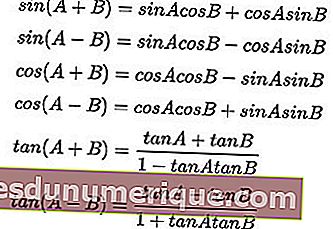
Fórmulas de multiplicação trigonométrica:
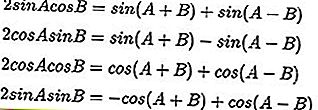
Fórmulas trigonométricas de soma e diferença:
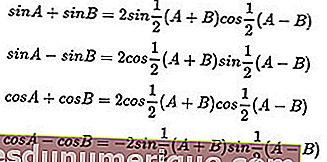
Exemplos de problemas de gatilho
Encontre o valor de 2 cos 75 ° cos 15 °:
Solução:
Com base nas informações do problema, podemos ver que o problema acima inclui a multiplicação trigonométrica. Use a fórmula de multiplicação para cos descrito acima, que é 2 cos A cos B = cos (A + B) + cos (A - B).
Responda:
2 cos 75 ° cos 15 ° = cos (75 +15) ° + cos (75 - 15) °
= cos 90 ° + cos 60 °
= 0 + ½
= ½
É uma coleção de fórmulas e problemas trigonométricos que você pode aprender e entender. Para poder entendê-lo melhor, você pode experimentar o PROBLEM, uma solução on-line ponderada e completa para praticar as questões de acordo com o currículo mais recente do Smart Class. Do ensino fundamental, médio ao ensino médio com diversas disciplinas como Matemática, Física, Química e outras. Aqui você pode aprender vários tipos de fórmulas completas com problemas de exemplo,
Vamos, o que você está esperando! Vamos tentar os exercícios PROBLEM no Smart Class agora.