Em matemática, um padrão de número é um arranjo de vários números que formam um certo padrão. Vários tipos de padrões de número incluem padrões pares, ímpares, aritméticos e geométricos. Hoje, vamos discutir dois tipos de padrões numéricos, ou seja, linhas geométricas e séries geométricas.
Uma linha geométrica é uma sequência de números composta de termos que têm proporções fixas. O primeiro termo da seqüência geométrica é denotado por a. A razão ou comparação entre dois termos é denotada por r.
As linhas geométricas podem ser formuladas da seguinte forma.
a, ar, ar2, ar3, ..., arn-
a = o primeiro termo da sequência geométrica
r = a razão entre os termos
n = sequência de termos
Para determinar o valor do enésimo termo ou razão, podemos usar a seguinte fórmula.
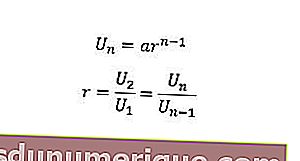
U n = o enésimo termo
Vamos trabalhar em um exemplo de problema abaixo.
Dada uma sequência geométrica 3, 9, 27, 81, 243. Com base nisso, determine a razão da sequência geométrica!
Sabemos U 1 = 3 e U 2 = 9, de modo que, se os colocarmos na fórmula, obteremos o seguinte resultado.
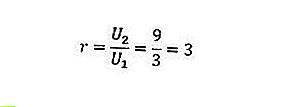
Portanto, a proporção ou comparação da sequência geométrica acima é 3.
(Leia também: Lógica Matemática, da Negação à Biimplicação)
Enquanto isso, uma série geométrica é a soma dos termos em uma sequência geométrica. Uma série geométrica pode ser denotada por S n, o que significa o número dos primeiros n termos na seqüência geométrica.
A série geométrica pode ser formulada da seguinte forma.

a = o primeiro termo da sequência geométrica
r = a razão entre os termos
n = sequência do último termo adicionado
U n = o enésimo termo
Vamos trabalhar em um exemplo de problema abaixo.
Dado que a série geométrica com o primeiro termo é 6 e o quarto termo é 48, então a soma dos primeiros seis termos é ...?
Sabemos que a = 6 e U 4 = 48. Se inserirmos a fórmula, o resultado será o seguinte.
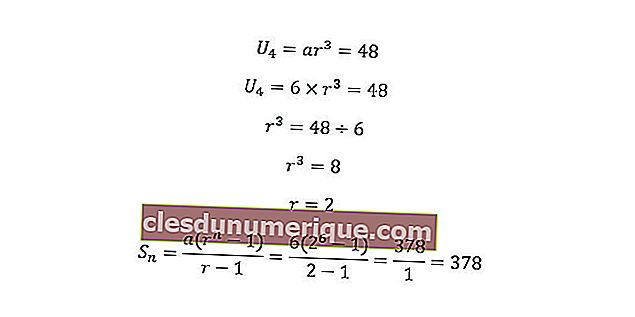
Portanto, a soma dos primeiros 6 termos da série acima é 378.