Círculo é um conjunto de pontos equidistantes de um ponto. As coordenadas desses pontos são determinadas pelo arranjo das equações circulares. Isso é determinado com base no comprimento do raio e nas coordenadas do centro do círculo.
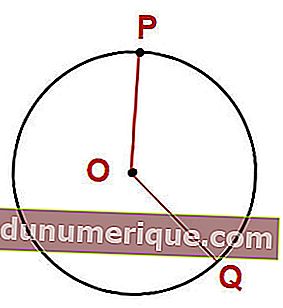
Na foto acima, podemos concluir que OP = OQ. O ponto O é chamado de centro do círculo, enquanto OP e OQ são os raios. Vamos considerar o seguinte exemplo.
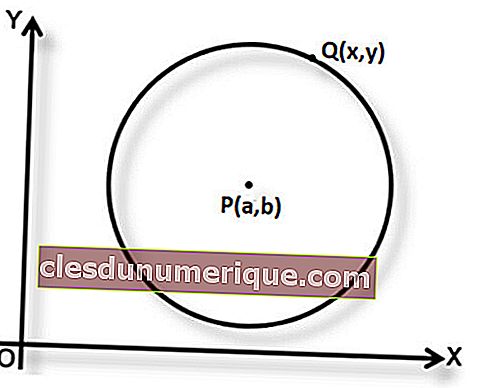
P (a, b) é o centro do círculo e o comprimento do raio é r. Se Q (x, y) é um ponto que fica no círculo, com base na definição do círculo pode-se concluir que PQ = r. A partir disso, podemos formular a equação do círculo com P (a, b) como o centro e r como o raio.
√ (x - a) 2 + (y - b) 2 = r
(x - a) 2 + (y - b) 2 = r2
Vamos trabalhar em um exemplo de problema abaixo.
Encontre a equação para o círculo cujo centro está no ponto (-5,4) cujo raio é 7!
A partir dessas afirmações, sabemos que a = -5, b = 4 er = 7. Se os inserirmos na equação, obteremos a seguinte resposta.
(x - (-5)) 2 + (y - 4) 2 = 72
(x + 5) 2 + (y - 4) 2 = 49
Que tal um círculo cuja coordenada central está em P (0,0)? A equação do círculo é a seguinte.
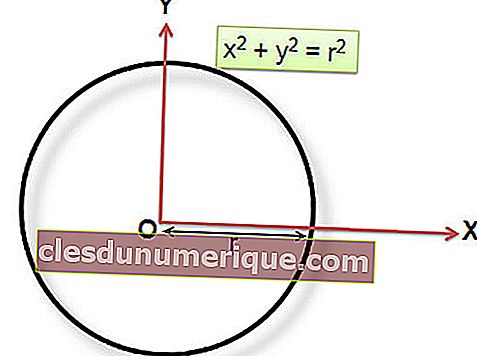
A forma geral da equação circular pode ser expressa nas seguintes formas.
(x - a) 2 + (y - b) 2 = r2, ou
X2 + y2 - 2ax - 2by + a2 + b2 - r2 = 0, ou
X2 + y2 + Px + Qy + S = 0, onde P = -2a, Q = -2b e S = a2 + b2 - r2
Condições para determinar a equação de um círculo
A equação circular contém três variáveis arbitrárias. A equação do círculo pode ser determinada se os valores das três variáveis forem conhecidos. Para descobrir os valores dessas três variáveis, uma das seguintes condições deve ser atendida:
- As coordenadas dos três pontos do círculo são conhecidas.
- As coordenadas de dois pontos no círculo conectados pelo diâmetro do círculo são conhecidas.
- As coordenadas do ponto central e as coordenadas do ponto do círculo são conhecidas.