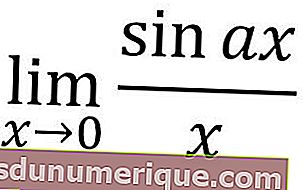O limite da função trigonométrica é definido como o valor mais próximo de um ângulo na função trigonométrica. Este cálculo pode ser substituído como o limite de uma função algébrica, mas por uma função trigonométrica que deve ser alterada primeiro.
A função trigonométrica deve ser convertida em uma identidade trigonométrica para um limite indefinido, que é um limite que, se substituído, será 0. Além disso, há também uma maneira de calcular um limite indefinido sem usar a identidade trigonométrica, mas usando o teorema do limite trigonométrico. Outros usam identidade e teorema simultaneamente.
Para determinar o valor limite das funções trigonométricas, existem várias maneiras que podem ser usadas, nomeadamente métodos numéricos, substituição, fatoração, tempos de pares e derivados.
(Leia também: Medindo a visibilidade usando fórmulas trigonométricas)
Mas com base no valor, podemos dividir essa fórmula em duas, ou seja, aquelas que estão próximas do número e próximas a zero.
X se aproximando de um número
Se tivermos o limite da função trigonométrica cujo x se aproxima do número c, podemos determinar seu valor substituindo c na função trigonométrica. As fórmulas são as seguintes.

X se aproximando do zero
Se o x do limite de uma função trigonométrica se aproxima de zero, podemos usar as fórmulas abaixo.

Se depois de substituir o valor x na função trigonométrica a forma for indefinida 0/0 ∞ / ∞, então para determinar o valor limite da função trigonométrica, você pode usar a regra de L'Hospital, a saber
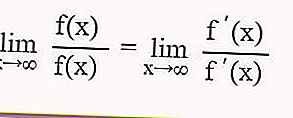
Compreensão da intuição dos limites da função trigonométrica
Compreender intuitivamente o limite de uma função trigonométrica é o mesmo que o limite de uma função algébrica. O limite da função trigonométrica existe se e somente se o limite esquerdo e o limite direito existem e o limite esquerdo é igual ao limite direito.