Você presta atenção se o telhado da casa e a barraca têm quase o mesmo formato? Se você olhar novamente, parece que consiste em 2 triângulos em cada extremidade, então cobertos por um cobertor retangular. Essa forma também é conhecida como prisma triangular. É chamado assim porque a base e a tampa são triangulares. Em geometria, estudaremos a definição e a fórmula dos prismas triangulares. Nesta ocasião, também discutiremos vários exemplos do problema, a fim de sermos capazes de compreender melhor este material.
Um prisma é uma forma que possui uma tampa e uma base com uma forma congruente de n lados, enquanto os lados verticais são retangulares.
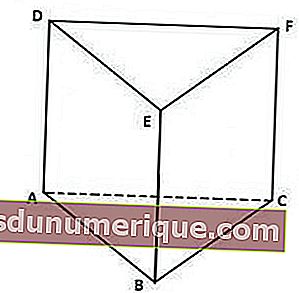
Os prismas triangulares têm as seguintes características:
Possui uma base triangular congruente e tampa.
Na imagem acima, a tampa do prisma, ou seja, o triângulo DEF, tem a mesma forma e tamanho do triângulo ABC como sua base.
Retângulo como lado vertical.
Como você pode ver, o prisma acima é limitado por três retângulos em cada lado da vertical, a saber, os retângulos ACFD, BCFE e ABED.
Possui 5 lados, 9 arestas e 6 vértices.
Os 5 lados de um prisma triangular consistem em 1 lado da base, 1 lado da tampa e 3 lados da vertical. Enquanto as 9 costelas consistem em 3 costelas verticais, 3 lados da base e 3 do lado da tampa. Além disso, os 6 vértices são pontos A, B, C, D, E e F.
Agora que conhecemos as características e também o significado de um prisma triangular, é hora de conhecermos as fórmulas do prisma triangular e exemplos de seus problemas.
Fórmulas de prisma triangular e exemplos de problemas
Haverá 2 tipos de fórmulas de prisma triangular que aprenderemos. A fórmula para encontrar o volume e a fórmula para encontrar a área da superfície. As fórmulas são assim:
Volume
Para o volume, usaremos a fórmula:
V = área da base × altura
ou
V = (½ x a x h) × altura do prisma
Então, para entender isso melhor, vamos dar uma olhada em um exemplo deste problema:
Um prisma tem 10 cm de altura. A base do prisma tem a forma de um triângulo retângulo com comprimentos laterais de 4 cm e 3 cm, respectivamente. Qual é o volume deste prisma triangular?
Solução:
Aqui, precisamos apenas inserir os números conhecidos em uma fórmula como esta:
V = (½ x a x h) × altura do prisma
V = (½ x 4 x 3) × 10
V = 6 × 10
V = 60 cm 3
Superfície
Ao calcular a área da superfície de um prisma triangular, usaremos uma fórmula como esta:
L = (2 x área da base) + (área de todos os lados perpendiculares)
se o triângulo for equilátero, você pode usar a fórmula:
L = (2 x área da base) + (3 x área de um lado da vertical)
Ou pode ser a fórmula:
L = (2 x área da base) + (perímetro da base x altura do prisma)
Vejamos um exemplo desse problema para ver como essa fórmula é aplicada. Aqui está um exemplo de problema:
Existe um prisma triangular equilátero que tem uma altura de 12 cm, um comprimento lateral de 5 cm e uma altura de 8 cm. Então, qual é a área da superfície deste prisma triangular?
Solução:
Para encontrar a área da superfície, simplesmente usamos a fórmula para a área da superfície de um prisma triangular como este:
L = (2 x área da base) + (3 x área de um plano vertical)
L = (2 x (½ x 5 x 8)) + (3 x (12 x 5))
L = 40 + 180
L = 220 cm 2
Essas são as várias fórmulas de prisma triangular que você deve conhecer, bem como alguns exemplos de problemas. Se ainda estiver confuso, você pode perguntar na coluna de comentários ou pode experimentar o Smart Class, a plataforma de tutoria online confiável do World.